- Forschen lernen
Die Wahl der korrekten Analyse
Mit statistischen Tests überprüfen Sie Ihre Hypothesen und können zeigen, ob beobachtete Muster zufällig entstanden sind oder nicht. Welcher der jeweils optimale Test ist, hängt von verschiedenen Faktoren ab.
14.10.2025

Unterschiedliche Forschungsfragen – von einfachen Mittelwertvergleichen bis hin zu komplexen Regressionsmodellen – erfordern unterschiedliche Tests, um Hypothesen zu prüfen, Unterschiede zwischen Gruppen auszuwerten oder Zusammenhänge zwischen Variablen zu untersuchen. Ohne tiefgehende Statistikkenntnisse kann die Entscheidung, welcher Test anzuwenden ist, jedoch herausfordernd sein. Einmal mehr empfehle ich deshalb, eine in solchen Fragen versierte Fachperson beizuziehen.
Um Sie optimal für die Besprechung mit der Statistikerin oder dem Statistiker Ihres Vertrauens vorzubereiten, diskutiere ich hier ein paar Grundlagen zum Thema der statistischen Testverfahren.
Zwei Klassen von statistischen Tests
Wir unterscheiden in der Inferenz-Statistik zwei grosse Klassen von statistischen Testverfahren:
- Parametrische Tests setzen voraus, dass die Daten einer bestimmten Verteilung – meistens der Normalverteilung – folgen. Typische Beispiele sind der t-Test, die Varianzanalyse (ANOVA) und lineare Regressionsverfahren.
- Nicht parametrische Tests benötigen keine Annahmen über die Verteilungsform, eignen sich bei ordinalen Daten, kleinen Stichproben oder wenn Normalität und Varianzhomogenität verletzt sind. Beispiele hierfür sind der Mann-Whitney-U-Test, der Kruskal-Wallis-Test und der Wilcoxon-Vorzeichen-Rang-Test.
Die Unterscheidung zwischen parametrischen und nicht parametrischen Verfahren muss bei der Wahl der Analyse stets berücksichtigt werden.
Entscheidungshilfe
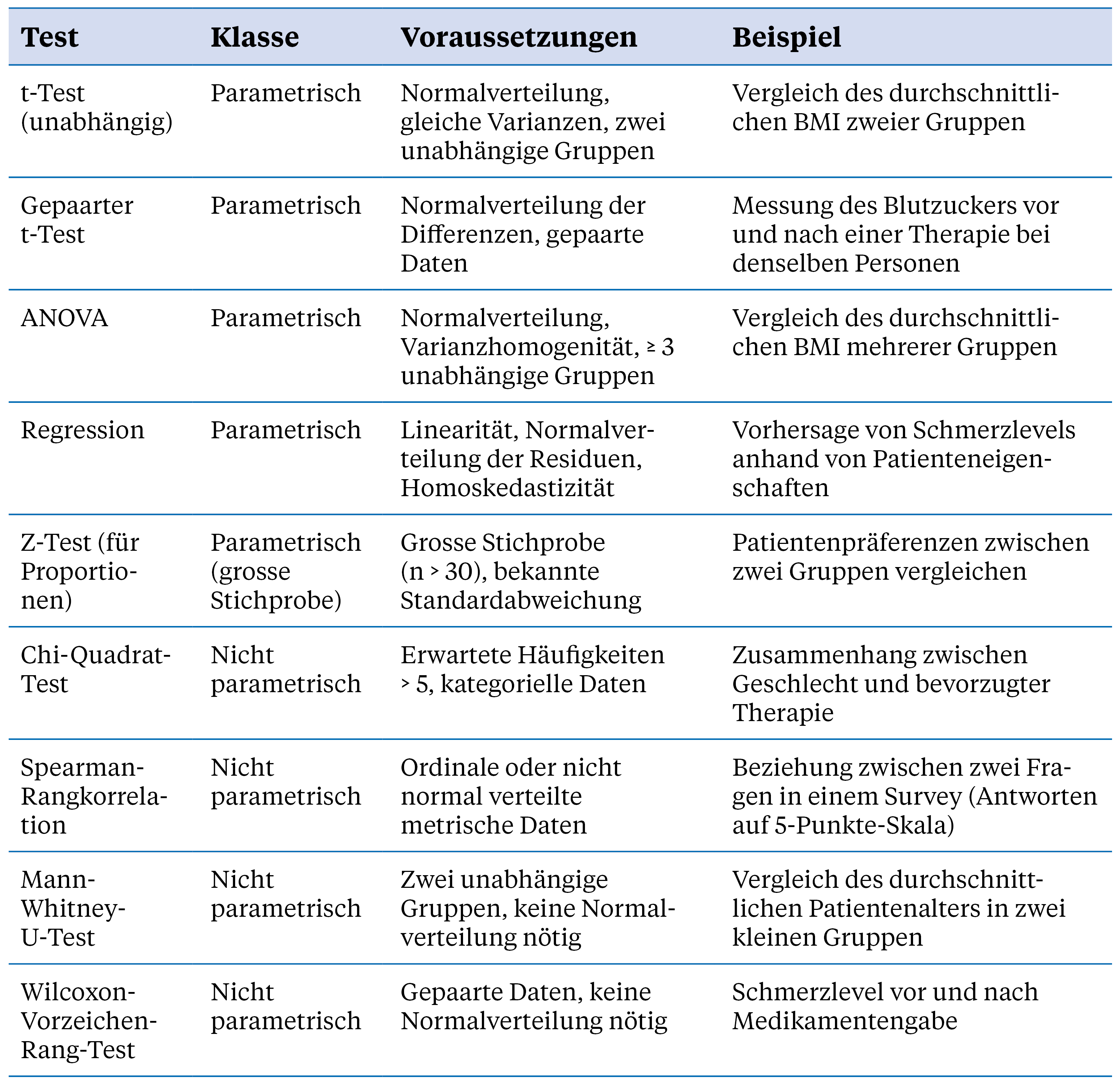
Die Beantwortung der folgenden zentralen Fragen hilft Ihnen, fundierte und nachvollziehbare Entscheidungen zu treffen sowie die statistische Analyse Ihrer Daten robust und effizient zu gestalten. Die Tabelle liefert ein paar ausgewählte Beispiele von häufig verwendeten Tests.
- Datentyp: Handelt es sich um quantitative oder kategorielle Daten?
- Bei quantitativen (kontinuierlichen) Daten analysieren wir deren Verteilung (z. B. Mittelwert, Streuung).
- Bei kategoriellen Daten (z. B. Geschlecht, Dukes-Stadium A–D) interessieren uns die Häufigkeiten der möglichen Kategorien.
- Anzahl der Gruppen: Werden zwei, drei oder mehr Gruppen verglichen?
- Unabhängigkeit der Beobachtungen: Sind die Stichproben unabhängig voneinander (ungepaarte Daten) oder abhängig (gepaart, z. B. durch zwei Messungen pro Individuum)?
- Verteilungsannahmen:
- Liegt eine Normalverteilung vor? Dies kann mit grafischen Mitteln (z. B. Q-Q-Plot) und Normalitätstests (z. B. Shapiro-Francia-Test) ermittelt werden.
- Ist die Varianz zwischen den Gruppen homogen (homoskedastisch)? Dies kann etwa mittels Boxplots geprüft werden.
- Stichprobengrösse: Wie gross ist Ihre Stichprobe? Nicht parametrische Verfahren sind bei kleinen Stichproben besonders geeignet, da sie robuster gegenüber Verletzungen der Normalitätsannahme sind.